
Pessoal, aqui é o Prof. Hugo Lima. Eu e o Prof. Arthur Lima resolvemos a prova da PF de Raciocínio Lógico e Estatística, para Agente, Escrivão e Papiloscopista. Aqui vocês vão ter acesso à nossa resolução da prova.
ASSISTA A CORREÇÃO DAS PROVAS NOS LINKS ABAIXO
Gabarito PF Raciocínio Lógico
CEBRASPE – PF – 2021) Para realizar uma operação de busca e apreensão, em duas localidades diferentes, devem ser deslocadas duas equipes, cada uma delas composta por 1 delegado, 1 escrivão e 2 agentes.
Tendo como base essas informações, julgue os itens seguintes.
( ) Se estiverem disponíveis, no momento da formação das equipes, exatamente, 2 delegados, 2 escrivães e 4 agentes, o número de maneiras distintas de se montar as duas equipes seria igual ao número de maneiras de se montar, escolhendo-se entre esses mesmos profissionais, uma única equipe para a realização de uma busca em uma única localidade.
Item correto. Ao montar uma equipe, a outra já estará montada pelos elementos que sobrarem.
( ) Se estiverem disponíveis, no momento da formação das equipes, exatamente, 2 delegados, 2 escrivães e 4 agentes, o número de maneiras distintas de se montar as duas equipes é igual a 4!.
Item correto. C(2,1) x C(2,1) x C(4,2) = 24
( ) Se estiverem disponíveis, no momento da formação das equipes, 3 delegados, 4 escrivães e 6 agentes, o número de maneiras distintas de se montar as duas equipes é superior a 6.500.
Item errado. C(3,1) x C(4,1) x C(6,2) = 180
CEBRASPE – PF – 2021) P1: Se a fiscalização for deficiente, as falhas construtivas não foram corrigidas.
P2: Se as falhas construtivas foram corrigidas, os mutuários não tiveram prejuízos.
P3: A fiscalização foi deficiente.
C: Os mutuários tiveram prejuízos.
Considerando um argumento formado pelas proposições precedentes, em que C é a conclusão, e P1 a P3 são as premissas, julgue os itens a seguir:
( ) O argumento apresentado não é válido.
Item correto. Partindo da proposição P3, que é simples, temos que ela é V. Levando essa informação a P1, o antecedente da condicional é V. Para que a premissa seja V, o consequente deve ser V. Levando essa informação em P2, o antecedente é F. Isso já garante que a premissa seja V, independentemente do valor lógico do consequente. Com isso, a conclusão C não decorre automaticamente quando as premissas são V. Ou seja, o argumento não é válido.
( ) A proposição P2 é equivalente a “Se as falhas construtivas não foram corrigidas, os mutuários tiveram prejuízos”.
Item errado. Sabemos que uma condicional p –> q é equivalente a ~q –> ~p. Não foi o caso mencionado.
( ) Caso o argumento apresentado seja válido, a proposição C será verdadeira.
Item errado. Se o argumento for válido, a proposição C será verdadeira se as premissas forem verdadeiras.
( ) A proposição P1 é equivalente a “Não é verdade que a fiscalização foi deficiente e que as falhas construtivas foram corrigidas”.
Item correto. Sabemos que a condicional p –> q é equivalente a ~p ou q. Assim obtemos: a fiscalização não foi deficiente ou as falhas construtivas não foram corrigidas. Podemos, ainda, colocar o “não” em evidência, obtendo: não é verdade que (a fiscalização foi deficiente e as falhas construtivas foram corrigidas).
( ) A tabela verdade da proposição condicional associada ao argumento tem menos de dez linhas.
Item correto. A tabela verdade terá 2³ = 8 linhas.
( ) Uma negação correta da proposição P1 pode ser expressa por: “Se a fiscalização não foi eficiente, as falhas construtivas foram corrigidas”.
Item errado. A negação da condicional p –> q é dada por p e ~q. Como foi dada uma condicional, o item está errado.
CEBRASPE – PF – 2021) Considere os seguintes conjuntos:
P = {todos os policiais federais em efetivo exercício no país}
P1 = {policiais federais em efetivo exercício no país e que têm até 1 ano de experiência no exercício do cargo}
P2 = {policiais federais em efetivo exercício no país e que têm até 2 anos de experiência no exercício do cargo}
P3 = {policiais federais em efetivo exercício no país e que têm até 3 anos de experiência no exercício do cargo}
e, assim, sucessivamente.
Com base nessas informações, julgue os itens que se seguem.
( ) O conjunto P é igual à união infinita dos conjuntos P1 , P2 , P3 , …
Item correto. Se juntarmos todos esses conjuntos, obtemos todos os policiais federais em efetivo exercício no país.
( ) P2 é subconjunto de P1.
Item errado. P1 é subconjunto de P2.
( ) Escolhendo-se aleatoriamente um integrante do conjunto P, a probabilidade de ele ter entre dois e três anos de experiência no exercício do cargo é dada por n(P2 – P3)/n(P3), em que n(X) indica o número de elementos do conjunto X e P2 – P3 é o conjunto formado pelos indivíduos que estão em P2, mas não estão em P3.
Item errado. O correto seria n(P3 – P2)/n(P).
Gabarito PF Estatística
CEBRASPE – PF – 2021) Considerando que o horário de ocorrência de certo tipo de crime em determinado local seja representado por uma variável aleatória contínua X, cuja função de densidade é escrita como
f(x) = γ (x – 12)2,
em que 0 ≤ x < 24 e γ é uma constante de normalização (γ>0), julgue os itens subsequentes.
( ) P(X=5) > γ.
Item errado. Como X é variável contínua, a probabilidade de X ser igual a 5 é zero. Além disso, γ>0. Ou seja, P(X=5) = 0 e não P(X=5) > 0.
( ) O valor da constante γ é inferior a 0,01.
Item correto. Integral de f(x)dx, de 0 a 24 = γ = 3/3456 < 3/3000 = 0,001.
( ) O valor esperado de X é igual a 12.
Item correto. E(X) = integral de xf(x)dx de 0 a 24 = 12. Trata-se de uma função de segundo grau, que toca o eixo x em x = 12, é simétrica e tem concavidade para cima. Então, graficamente, podemos dizer que a média vai estar sobre o 12.
CEBRASPE – PF – 2021) Considere que X e Y sejam variáveis aleatórias contínuas que se distribuem conjuntamente conforme a função de densidade
f(x,y) = x + y,
na qual 0 < x < 1 e 0 < y < 1.
Com base nessas informações, julgue os itens seguintes.
( ) E [X + Y|X = 1/2] = 14/12.
Item errado. É possível mostrar que E [X + Y|X = 1/2] = integral de (x+y)f(x,y)dy de 0 a 1, obtendo 13/12.
( ) X e Y são variáveis aleatórias independentes.
Item errado. Para verificar se são independentes, f(x,y) = g(x)h(y) em que g e h são as funções marginais. É possível obter g(x) = x + 1/2 e h(y) = y + 1/2. Como f(x,y) ≠ g(x)h(y) não podemos dizer que são variáveis independentes.
( ) Y é uma variável aleatória uniforme no intervalo (0,1).
Item errado. A função marginal para y é h(y) = y + 1/2. Portanto, percebe-se que essa função varia com y. Não podemos dizer que é uniforme.
CEBRASPE – PF – 2021) Um estudo objetivou avaliar a evolução do número mensal Y de milhares de ocorrências de certo tipo de crime em determinado ano. Com base no método dos mínimos quadrados ordinários, esse estudo apresentou um modelo de regressão linear simples da forma
Y = 5 – 0,1 x T,
em que Y representa a reta ajustada em função da variável regressora T, tal que 1 ≤ T ≤ 12.
Os erros padrão das estimativas dos coeficientes desse modelo, as razões t e seus respectivos p-valores encontram-se na tabela a seguir.
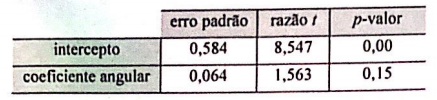
Os desvios padrão amostrais das variáveis Y e T foram, respectivamente, 1 e 3,6.
Com base nessas informações, julgue os itens a seguir.
( ) A correlação linear entre as variáveis Y e T foi igual a -0,1.
Item errado. Beta = R x desvio padrão Y/desvio padrão X. Com isso, R = -0,36.
( ) Se a média amostral da variável T for igual a 6,5, então a média amostral da variável Y será igual a 4,35 mil ocorrências.
Item correto. Y = 5 – 0,1 x 6,5 = 4,35.
( ) Considere que a denote o coeficiente angular do modelo de regressão linear simples e considere, ainda que o teste de hipóteses H0: a = 0 versus H1: a ≠ 0. Nessa situação, com referência a esse teste, caso o nível de significância escolhido seja igual a 5%, os resultados do estudo em questão indicarão que não há evidências estatísticas contra a hipótese nula H0: a = 0.
Item correto. Quando p-valor é maior que o nível de significância, não podemos rejeitar a hipótese nula.
CEBRASPE – PF – 2021)

Considerando que o conjunto de dados apresentado represente uma realização de uma amostra aleatória simples de tamanho n= 5 retirada de uma população X, cuja função de probabilidade acumulada é escrita como
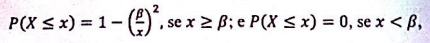
em que β é o parâmetro desconhecido, julgue os itens que se seguem.
( ) A média amostral é uma estatística suficiente para a estimação do parâmetro β.
Item correto. Considerando que a média da distribuição de x é igual a 2β, teoricamente a média amostral de x seria mesmo uma estatística suficiente pra estimar beta.
( ) A estimativa de máxima verossimilhança para o parâmetro β é igual ou superior a 3,5.
Item errado. É possível chegar a β = 1,92.
( ) Pelo método dos mínimos quadrados ordinários, a estimativa da média populacional é igual ou superior a 3,5.
Item correto. Média amostral é de 3,84. Basta somar as observações e dividir por 5.
Assinatura Ilimitada
Prepare-se para a sua aprovação de maneira mais ágil, enxuta e completa com o incrível PDF 2.0: fruto da parceria entre Direção e Qconcursos, a plataforma proporciona uma nova experiência em estudos para concursos, totalmente integrada, com tecnologia avançada e que te dará a segurança de estar a cada dia mais próximo do seu sonho.

