Gabarito ISS Guarulhos – Raciocínio Lógico – prova resolvida

Caros alunos, vejam o meu gabarito ISS Guarulhos de Raciocínio Lógico, bem como a prova resolvida com os meus comentários. Espero que tenham ido muito bem!

Gabarito ISS Guarulhos Raciocínio Lógico – prova resolvida

VUNESP – ISS/Guarulhos – 2019) Considere as afirmações e seus respectivos valores lógicos.

I. Maria é uma excelente enfermeira. FALSA.

II. Joel não é um carpinteiro. VERDADEIRA.

III. Paulo é um cantor de pagode. VERDADEIRA.

IV. Sandra não é uma analista competente. FALSA.

A alternativa que apresenta uma proposição composta verdadeira é

(A) Se Paulo é um cantor de pagode, então Maria é uma excelente enfermeira.

(B) Joel não é um carpinteiro e Sandra não é uma analista competente.

(C) Paulo não é um cantor de pagode ou Sandra é uma analista competente.

(D) Se Maria não é uma excelente enfermeira, então Sandra não é uma analista competente.

(E) Joel é um carpinteiro ou Paulo não é cantor de pagode.

RESOLUÇÃO:

Vejamos como ficam os valores lógicos de cada proposição:

a) V –> F é uma condicional falsa

b) V e F é uma conjunção falsa

c) F ou V é uma disjunção verdadeira

d) V –> F é uma condicional falsa

e) F ou F é uma disjunção falsa

Resposta: C

VUNESP – ISS/Guarulhos – 2019) Dentre as sentenças a seguir, aquela que é uma sentença aberta é

(A) 3 ⋅ x + 4 – x – 3 – 2 ⋅ x = 0

(B) 7 + 3 = 11

(C) 0 ⋅ x = 5

(D) 13 ⋅ x = 7

(E) 43 – 1 = 42

RESOLUÇÃO:

               Para termos uma sentença aberta, é preciso que, a depender do valor da variável x, a sentença possa ser V ou F. Note que as alternativas B e E apresentam proposições, pois sequer possuem variáveis. Na alternativa A, a variável x é cancelada, afinal 3x – x – 2x = 0. Deste modo, o valor de x não interfere em A, sendo esta uma proposição.

               Na alternativa C, como zero vezes qualquer número é igual a zero, fica evidente que a proposição 0.x = 5 é falsa para qualquer valor de x.

               Na alternativa D nós temos um caso onde, a depender do valor de x, a frase pode ser V ou F. Se x = 7/13, a frase é V. Caso contrário, é F. Esta é uma sentença aberta.

Resposta: D

VUNESP – ISS/Guarulhos – 2019) Considere verdadeiras as afirmações a seguir.

I. Todos os funcionários são economistas.

II. Há economista que também é administrador.

A partir dessas afirmações, assinale a alternativa correta.

(A) Os administradores que não são economistas são funcionários.

(B) Qualquer economista é funcionário.

(C) É possível que haja funcionário que não seja economista.

(D) Os administradores que são economistas são funcionários.

(E) Os funcionários que são administradores são economistas.

RESOLUÇÃO:

Vamos avaliar cada alternativa de resposta:

(A) Os administradores que não são economistas são funcionários.

               Como todos os funcionários são economista, aqueles administradores que não são economistas NÃO podem ser funcionários. Item FALSO.

(B) Qualquer economista é funcionário.

               O fato de todo funcionário ser economista não permite garantir que todo economista é funcionário. Item FALSO.

(C) É possível que haja funcionário que não seja economista.

               Falso, pois todo funcionário é economista.

(D) Os administradores que são economistas são funcionários.

               Falso, pois podem existir administradores que são economistas e NÃO atuam na empresa.

(E) Os funcionários que são administradores são economistas.

               Verdadeiro, pois todo funcionário é economista (inclusive aqueles que também são administradores).

Resposta: E

VUNESP – ISS/Guarulhos – 2019) Considere as operações entre conjuntos:

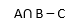
A alternativa cuja parte sombreada corresponde ao resultado dessas operações é

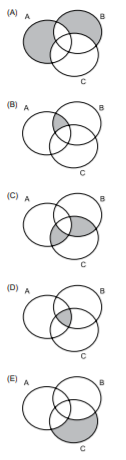
RESOLUÇÃO:

               A expressão (A e B) – C é obtida pegando-se a interseção entre os conjuntos A e B e, desta interseção, retirando aquela parte que também está presente no conjunto C.

               Temos isso na figura da alternativa B.

Resposta: B

VUNESP – ISS/Guarulhos – 2019) A alternativa que corresponde à negação lógica da proposição composta: “todos os cantores são músicos e existe advogado que é cantor”, é:

(A) Nenhum cantor é músico e não existe advogado que seja cantor.

(B) Pelo menos um cantor não é músico ou não existe advogado que seja cantor.

(C) Há cantores que são músicos e existe advogado que não é cantor.

(D) Nenhum cantor é músico ou não existe advogado que seja cantor.

(E) Pelo menos um cantor não é músico ou existe advogado que é cantor.

RESOLUÇÃO:

               A negação de uma conjunção é obtida negando-se as duas proposições e trocando-se o “e” pelo “ou”. Para negar “todos os cantores são músicos” basta mostrar que “algum cantor NÃO é músico”. E para negar que “existe advogado que é cantor” basta mostrar que “nenhum advogado é cantor”. Assim, temos:

“Algum cantor NÃO é músico OU nenhum advogado é cantor”

               Uma variação disto é:

Pelo menos um cantor não é músico ou não existe advogado que seja cantor

Resposta: B

VUNESP – ISS/Guarulhos – 2019) A alternativa que corresponde à equivalente lógica da proposição composta: “se as frutas estão maduras, então é tempo de colheita”, é:

(A) as frutas não estão maduras ou é tempo de colheita.

(B) se não é tempo de colheita, então as frutas estão maduras.

(C) as frutas estão maduras, e é tempo de colheita.

(D) não é tempo de colheita, e as frutas não estão maduras.

(E) se é tempo de colheita, então as frutas estão maduras.

RESOLUÇÃO:

               A condicional p–>q equivale à disjunção ~p ou q, que é obtida negando-se a primeira proposição e mantendo-se a segunda. Ficamos com

“As frutas NÃO estão maduras OU é tempo de colheita”

Resposta: A

VUNESP – ISS/Guarulhos – 2019) Considere os conjuntos:

F = {1,2,3,4,5,6}

G = {2,4,6,8,10,12}

H = {1,2,3,10,11,12}

J = {3,4,5,6,7,8}

Sabe-se que

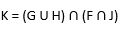
O conjunto é igual a

(A) K = {1,2,4,5,6}

(B) K = {4,5,6}

(C) K = {1,2,4,5,6,10}

(D) K = {3,4,6}

(E) K = {4,6}

RESOLUÇÃO:

               Podemos começar escrevendo G U H, ou seja, unindo os conjuntos G e H:

G U H = {1, 2, 3, 4, 6, 8, 10, 11, 12}

               Podemos também fazer a interseção entre F e J:

F e  J = {3, 4, 5, 6}

               Agora podemos fazer a interseção entre os dois conjuntos acima:

K = {3, 4, 6}

Resposta: D

VUNESP – ISS/Guarulhos – 2019) Considere verdadeiras as afirmações.

I. Se Arnaldo é grosseiro, então Beatriz é gentil.

II. Se Cátia é educada, então Arnaldo não é grosseiro.

III. Se Arnaldo não é grosseiro, então Deise é amável.

IV. Deise não é amável.

A partir dessas afirmações, é correto concluir que:

(A) Beatriz não é gentil ou Cátia é educada.

(B) Arnaldo é grosseiro e Cátia é educada.

(C) Beatriz não é gentil ou Cátia não é educada.

(D) Cátia é educada ou Arnaldo não é grosseiro.

(E) Beatriz é gentil e Arnaldo não é grosseiro.

RESOLUÇÃO:

               Como IV é uma proposição simples, começamos por ela, vendo que DEISE NÃO É AMÁVEL. Em III, como a segunda parte da condicional é F, a primeira deve ser F também, de modo que ARNALDO É GROSSEIRO. Em II, como a segunda parte da condicional é F, a primeira deve ser F também, de modo que CÁTIA NÃO É EDUCADA. Em I, como a primeira parte é V, a segunda deve ser V também, de modo que BEATRIZ É GENTIL.

               Considerando as conclusões em letras maiúsculas, podemos marcar a alternativa C, que é uma disjunção do tipo “F ou V”, ou seja, é verdadeira.

Resposta: C

VUNESP – ISS/Guarulhos – 2019) Considere as afirmações:

I. Se o diretor é forte, então o secretário é fraco ou o diretor é forte.

II. João é alto ou Paulo é gordo e João não é alto e Paulo não é gordo.

III. Carlos não é tímido e, se Pedro é expansivo, então Carlos é tímido.

Na ordem em que estão expressas, as afirmações são, respectivamente, uma

(A) tautologia, contradição e contingência.

(B) contingência, contradição e tautologia.

(C) contradição, tautologia e contingência.

(D) contingência, tautologia e contradição.

(E) tautologia, contingência e contradição.

RESOLUÇÃO:

               Em I temos:

(diretor forte) –> (secretário fraco ou diretor forte)

               Repare que, se a primeira parte desta condicional for V, a segunda será V também (pois basta “diretor forte” ser V para a disjunção ficar verdadeira). Logo, nunca é possível deixar esta condicional V–>F, o que mostra que ela é sempre verdadeira. Isto é, temos uma TAUTOLOGIA.

               Em II temos:

(João alto ou Paulo gordo) e (João não alto e Paulo não gordo)

               Veja que é possível deixar esta frase falsa, bastando para isto que alguma das proposições simples do segundo parênteses seja F. Caso as duas proposições simples do segundo parênteses sejam V, as duas do primeiro parênteses serão F. Assim, não é possível deixar a frase verdadeira. Temos uma CONTRADIÇÃO.

               Em III temos:

(Carlos não tímido) e (Pedro expansivo –> Carlos tímido)

               Esta frase pode ficar F, bastando que ‘Carlos não tímido’ seja F. E pode ficar verdadeira, caso ‘Carlos não tímido’ seja V e ‘Pedro expansivo’ seja F. Temos uma CONTINGÊNCIA.

Resposta: A

VUNESP – ISS/Guarulhos – 2019) Considere os argumentos a seguir.

I. O dobro de um número é um número par. O dobro de 1,5 é 3. Logo, o número 3 é um número par.

II. Todos os atletas são fortes. Juca é forte. Logo, Juca é atleta.

III. Os cachorros têm quatro patas. As vacas têm quatro patas. Logo, as vacas são cachorros.

Na ordem em que estão expressas, os argumentos são, respectivamente,

(A) válido, válido e inválido.

(B) inválido, inválido e válido.

(C) válido, inválido e inválido.

(D) inválido, inválido e inválido.

(E) válido, inválido e válido.

RESOLUÇÃO:

               Vejamos cada argumento:

I. O dobro de um número é um número par. O dobro de 1,5 é 3. Logo, o número 3 é um número par.

               Se admitirmos que o dobro de um número é par, e que 3 é o dobro de 1,5, precisamos ACEITAR  a conclusão de que 3 é par. O argumento é VÁLIDO.

II. Todos os atletas são fortes. Juca é forte. Logo, Juca é atleta.

               Se admitirmos que todo atleta e forte e que Juca é forte, ainda assim NÃO precisamos aceitar que Juca é atleta (pois nada garante que somente os atletas é que são fortes). O argumento é INVÁLIDO.

III. Os cachorros têm quatro patas. As vacas têm quatro patas. Logo, as vacas são cachorros.

               Se admitirmos que os cachorros e as vacas tem 4 patas, ainda assim NÃO precisamos aceitar que vacas são cachorros, pois pode haver mais de um tipo de animal com o mesmo número de patas. O argumento é INVÁLIDO.

Resposta: C

Saudações,

Prof. Arthur Lima

Confira o Gabarito Consolidado com TODAS as matérias

Veja também o gabarito de Direito Empresarial

Veja também o gabarito de Português

Veja também o gabarito de Direito Constitucional

Veja também o gabarito de Direito Tributário

Veja também o gabarito de Direito Penal

Veja também o gabarito de Contabilidade

Veja também o gabarito de Direito Administrativo

Veja também o gabarito de Informática/TI

Veja também o gabarito de SIMPLES NACIONAL