Teste ANPAD Setembro/2021 – Inscrições abertas

Olá pessoal. O TESTE ANPAD – Edição Setembro/2021 está com inscrições abertas. Você tem até 20/08/2021 para fazer sua inscrição. A realização do teste ocorrerá apenas em 26/09/2021.

Com isso você tem tempo suficiente para se preparar com a gente para o próximo teste Anpad.

Não deixe de conferir nossos cursos para a ANPAD:

550 questões resolvidas (em PDF) de Raciocínio Lógico, Analítico e Quantitativo para Teste ANPAD

Raciocínio Quantitativo (Teoria e 259 questões Anpad resolvidas) para Teste ANPAD – Orientação Acadêmica

Raciocínio Lógico e Raciocínio Analítico (Teoria e 331 questões Anpad resolvidas) para Teste ANPAD – Orientação Acadêmica

No artigo de hoje, vamos resolver a prova de raciocínio lógico e quantitativo da Edição de Junho 2021. Temos uma anulação na questão 11. Vamos ao trabalho?

• ANPAD – 2021)

Considere a seguinte proposição: O carro de Matilde não é azul, nem é pequeno, mas João está em casa ou está com fome. Mediante a escolha conveniente de proposições lógicas simples p, q, c e f, a proposição acima foi simbolicamente representada por:

[~(p v q)] ^ [c v (~f)]

Sabe-se que as proposições lógicas p e c escolhidas foram definidas por:

p: O carro de Matilde é pequeno.

c: João está em casa.

Além disso, sabe-se que as proposições q e f se debruçam, exclusivamente, sobre a cor do carro e a eventual fome de João, respectivamente.

Nesses termos, a proposição  f –> (~q) é logicamente equivalente à proposição:

a) Para que o carro de Matilde seja azul, é necessário que João esteja com fome.

b) Para que o carro de Matilde não seja azul, é necessário que João esteja com fome.

c) Para que o carro de Matilde não seja azul, é necessário que João não esteja com fome.

d) Para que o carro de Matilde seja azul, é suficiente que João não esteja com fome.

e) Para que o carro de Matilde não seja azul, é suficiente que João não esteja com fome.

RESOLUÇÃO:

Reescrevendo a proposição do enunciado, temos: o carro de Matilde não é azul E o carro de Matilde não é pequeno E João está em casa OU João está com fome.

Podemos dizer ainda: ~(o carro de Matilde é azul OU o carro de Matilde é pequeno) E João está em casa OU ~(João não está com fome).

Como q é sobre a cor do carro, podemos dizer que q é: o carro de Matilde é azul.

Como f é sobre a fome de João, podemos dizer que f é: João não está com fome.

Assim, a proposição f –> ~q é dada por:

Se João não está com fome, então o carro de Matilde não é azul.

Aqui, f é uma condição suficiente para ~q.

Assim, podemos dizer que Para que o carro de Matilde não seja azul, é suficiente que João não esteja com fome.

Resposta: E

• ANPAD – 2021)

Considere os seguintes argumentos:

O argumento válido é aquele numerado com

a) 4

b) 1

c) 2

d) 3

e) 5

RESOLUÇÃO:

Vamos analisar cada argumento, forçando a conclusão a ser falsa e tentando obter premissas V.

Argumento 1:

Conclusão ~B é F, ou seja, B é V.

Vamos supor que a premissa A seja V.

Logo, na primeira premissa, temos:

(A ^(~B)) v ((~A) ^ B) = (V ^ F) v (F ^ V) = F v F = F.

Portanto, ao forçar a conclusão a ser falsa, não conseguimos obter premissas verdadeiras, o que mostra que o argumento é válido.

Argumento 2:

Conclusão B é F.

Vamos supor que a premissa A seja V.

Logo, na primeira premissa, temos:

(A ^ B) v (A v B) = (V ^ F) v (V v F) = F v V = V

Portanto, ao forçar a conclusão a ser falsa, foi possível obter premissas V, o que mostra que o argumento é inválido.

Argumento 3:

Conclusão ~B é F, ou seja, B é V.

Vamos supor que a premissa ~A seja V, ou seja, A é F.

Logo, na primeira premissa, temos:

A –> B, que é F –> V, que é V

Portanto, ao forçar a conclusão a ser falsa, foi possível obter premissas V, o que mostra que o argumento é inválido.

Argumento 4:

Conclusão B é F.

Vamos supor que a premissa A seja V.

Logo, na primeira premissa, temos:

B –> A, que é F –> V, que é V.

Portanto, ao forçar a conclusão a ser falsa, foi possível obter premissas V, o que mostra que o argumento é inválido.

Argumento 5:

Conclusão ~B é F, ou seja, B é V.

Vamos supor que a premissa A seja V.

Logo, na primeira premissa, temos:

(A ^ B) v (~B) = (V ^ V) v (F) = V v F = V

Portanto, ao forçar a conclusão a ser falsa, foi possível obter premissas V, o que mostra que o argumento é inválido.

Resposta: B

• ANPAD – 2021)

A seguir são mostrados os primeiros quatro termos de uma sequência cuja evolução perpassa a inclusão de letras, seguindo a ordem alfabética, em quantidades iguais à ordem do respectivo termo na sequência.

Primeiro termo: A

Segundo termo: AABB

Terceiro termo: AAABBBCCC

Quarto termo: AAAABBBBCCCCDDDD

No termo formado por um total de 324 letras, quantas letras T há?

a) 18

b) 19

c) 0

d) 324

e) 20

RESOLUÇÃO:

    No primeiro termo temos uma letra A. No segundo termo, temos 2 A e 2 B. No terceiro termo, temos 3 A, 3B e 3C. No quarto termo, temos 4 A, 4B, 4C e 4D.

O número de letras por termo varia conforme a seguinte sequência: 1, 4, 9, 16, …

Veja que só temos quadrados perfeitos. Portanto, o termo 324, que é igual a 18², se refere ao décimo oitavo termo. Nele, teremos 18 A, 18 B, 18 C, …. e 18 R. Ou seja, não chegamos no T. Portanto, há zero letras T.

Resposta: C

• ANPAD – 2021)

Seja A o conjunto definido por A = {1,2,3,4,5,6,7,8,9,10}.

Quantos são os subconjuntos de A que possuem 2 ou mais elementos?

a) 1054

b) 1013

c) 45

d) 40320

e) 1064

RESOLUÇÃO:

    Como temos 10 elementos, o número de conjuntos das partes de A será dado por 2¹⁰ = 1024. Esse total inclui todos os possíveis subconjuntos de A. No entanto, estamos interessados apenas naqueles subconjuntos que possuem 2 ou mais elementos. Assim, excluímos os subconjuntos formados por cada elemento sozinho, que são 10, e também o subconjunto vazio, totalizando 11. Assim, 1024 – 11 = 1013 subconjuntos.

Resposta: B

• ANPAD – 2021)

Pedro e Joana estão hospedados num hotel que, todos os dias, oferece aos seus hóspedes uma escolha de almoço e várias atividades e passeios, como, por exemplo, aulas de surfe, aulas de caiaque ou prática de escalada. Os hóspedes podem participar de quantas atividades quiserem num mesmo dia, podendo, inclusive, não ter participação alguma em atividades. Há no cardápio um almoço especial de frutos do mar, oferecido apenas aos hóspedes que participarem das aulas de surfe ou caiaque.

Sabendo que, num certo dia, Pedro almoçou o prato de frutos do mar e Joana almoçou um prato de filé e praticou escalada, afirma-se o seguinte sobre esse dia:

I. Pelo menos um dos hóspedes não fez aulas de surfe ou caiaque.

II. Pedro não praticou escalada.

III. Pelo menos um dos hóspedes fez aulas de surfe ou caiaque.

É verdade o que se afirma em:

a) I e II, apenas.

b) I, apenas.

c) II e III, apenas.

d) I, II e III.

e) III, apenas.

RESOLUÇÃO:

    Pedro almoçou frutos do mar, ou seja, ele participou das aulas de surfe ou caiaque nesse dia.

Joana almoçou um prato de filé e praticou escalada.

Analisando as alternativas, temos:

I. Pelo menos um dos hóspedes não fez aulas de surfe ou caiaque.

Sabemos que Pedro participou das aulas de surfe ou caiaque. Quanto à Joana, nada impede que ela tenha participado das aulas de surfe ou caiaque, uma vez que os hóspedes podem participar de quantas atividades quiserem num mesmo dia.

II. Pedro não praticou escalada.

Sabemos que Pedro participou das aulas de surfe ou caiaque. No entanto, nada impede que ele tenha participado da aula de escalada, uma vez que os hóspedes podem participar de quantas atividades quiserem num mesmo dia.

III. Pelo menos um dos hóspedes fez aulas de surfe ou caiaque.

Com certeza. Pedro almoçou frutos do mar, ou seja, ele participou das aulas de surfe ou caiaque nesse dia.

Resposta: E

• ANPAD – 2021)

De modo geral, uma potência a^x, a > 0, x ∈ Q₊ , é representável por meio de radicais (raízes), o que a torna mais facilmente calculável. No entanto, quando o expoente x da referida potência é um número irracional, as coisas ficam mais difíceis. Uma saída é considerar números racionais próximos do expoente irracional x e, em seguida, utilizar radicais para representar as potências aproximantes, mais facilmente calculáveis.

Considere a potência 2^π, por exemplo.

Poderíamos aproximar essa potência da forma citada, por meio do radical

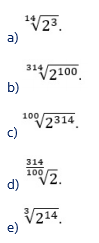
RESOLUÇÃO:

Vamos supor que π = 3,14 = 314/100. Logo:

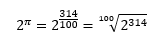
Resposta: C

• ANPAD – 2021)

Durante dois meses, determinado capital teve seu valor real depreciado mensalmente por uma mesma taxa T. A fim de corrigir o valor real inicial do capital, deve-se dar um aumento de 56,25% sobre o seu valor nominal atual.

A taxa de depreciação T é de

a) 20%.

b) 21,875%.

c) 28,125%.

d) 64%.

e) 80%.

RESOLUÇÃO:

Imagine que o capital inicial seja 100 reais. Ao final do primeiro mês, sofrendo depreciação a uma taxa T, obtemos 100 – 100 x T.

Ao final do segundo mês, sofrendo depreciação a uma taxa T, obtemos:

100 – 100 x T – (100 – 100 x T)T =

100 – 100 T – 100 T + 100 T² =

100 T²  – 200 T + 100

Se a esse valor acima for aplicado um aumento de 56,25%, retornamos ao valor original de 100:

(100 T²  – 200 T + 100) x 1,5625 = 100

156,25 T² – 312,5 T + 156,25 – 100 = 0

156,25 T² – 312,5 T + 56,25 = 0               (÷ 156,25)

T² – 2 T + 0,36 = 0              

Δ= (-2)² – 4(1)(0,36) = 2,56

T = (2 ± 1,6)/2

T₁ = 1,8 (descartamos)

T₂ = 0,2 = 20% (esse é o gabarito)

Resposta: A

• ANPAD – 2021)

Sabendo que A, B e C são proposições lógicas simples, analise as equivalências abaixo.

I. ((A –> B) v (A –> C)) <–> (A –> (B v C)).

II. ((A –> C) ^ (B –> C)) <–> ((A v B) –> C).

III. ((A –> B) ^ (B –> C)) <–> (A –> C).

São tautologias as equivalências em:

a) II, apenas.

b) I, apenas.

c) II e III, apenas.

d) I, II e III.

e) I e II, apenas.

RESOLUÇÃO:

Montando a tabela-verdade de cada equivalência, temos:

I. ((A –> B) v (A –> C)) <–> (A –> (B v C))

A	B	C	A –> B	A –> C	(A –> B) v (A –> C)	B v C	A –> (B v C)	I
V	V	V	V	V	V	V	V	V
V	V	F	V	F	V	V	V	V
V	F	V	F	V	V	V	V	V
V	F	F	F	F	F	F	F	V
F	V	V	V	V	V	V	V	V
F	V	F	V	V	V	V	V	V
F	F	V	V	V	V	V	V	V
F	F	F	V	V	V	F	V	V

II. ((A –> C) ^ (B –> C)) <–> ((A v B) –> C)

A	B	C	A –> C	B –> C	(A –> C) ^ (B –> C)	A v B	(A v B) –> C	II
V	V	V	V	V	V	V	V	V
V	V	F	F	F	F	V	F	V
V	F	V	V	V	V	V	V	V
V	F	F	F	V	F	V	F	V
F	V	V	V	V	V	V	V	V
F	V	F	V	F	F	V	F	V
F	F	V	V	V	V	F	V	V
F	F	F	V	V	V	F	V	V

III. ((A –> B) ^ (B –> C)) <–> (A –> C)

A	B	C	A –> B	A –> C	B –> C	(A –> B) ^ (B –> C)	III
V	V	V	V	V	V	V	V
V	V	F	V	F	F	F	V
V	F	V	F	V	V	F	F
V	F	F	F	F	V	F	V
F	V	V	V	V	V	V	V
F	V	F	V	V	F	F	F
F	F	V	V	V	V	V	V
F	F	F	V	V	V	V	V

Temos tautologia em I e II, apenas.

Resposta: E

• ANPAD – 2021)

Sejam x e y números tais que x⁴ + y⁴ = 10 e xy = √3.

O número x² + y² é igual a:

a) 5.

b) √13.

c) √10.

d) 4.

e) 16.

RESOLUÇÃO:

Acompanhe o desenvolvimento abaixo:

(x² + y²)² = x⁴ + 2x²y² + y⁴ = x⁴ + y⁴ + 2x²y² = 10 + 2(xy)² = 10 + 2(√3)² = 10 + 2 x 3 = 16

(x² + y²)² = 16

x² + y² = 4

Resposta: D

• ANPAD – 2021)

Sobre os alunos de Administração inscritos na turma C da disciplina de Métodos Matemáticos de certa universidade, sabe-se que todos que já cursaram a disciplina de Cálculo cursaram também a disciplina de Lógica. Além disso, é sabido que um dos inscritos possui terceiro grau completo, sendo formado em Psicologia. Considere os predicados P, Q e R e o conjunto universo U dados abaixo.

U = {x | x é um aluno de Administração inscrito na turma C}.

P(x): x tem terceiro grau completo.

Q(x): x já cursou a disciplina de Lógica.

R(x): x já cursou a disciplina de Cálculo.

A sentença que é logicamente equivalente às informações dadas sobre os alunos é:

a) (∀x P(x)) v (∀x (R(x) –> Q(x)))

b) (∃x P(x)) v (∀x (Q(x) –> R(x)))

c) (∃x P(x)) ^ (∀x (R(x) –> Q(x)))

d) (∃x P(x)) ^ (∃x (Q(x) –> R(x)))

e) (∀x P(x)) v (∃x (R(x) –> Q(x)))

RESOLUÇÃO:

Veja que existe um inscrito que possui terceiro grau completo. Assim devemos procurar por ∃x P(x), o que nos faz descartar as alternativas a e b.

A isso podemos adicionar (conjunção) a informação de que, qualquer que seja o aluno x, se ele cursou cálculo, então cursou lógica: ∀x (R(x) –> Q(x))

Encontramos isso corretamente expresso na alternativa C.

Resposta: C

• ANPAD – 2021)

Dos 60 hóspedes de um hotel, sabe-se que:

I. 20 se hospedaram desacompanhados.

II. 30 eram do sexo feminino.

III. 18 eram menores de idade.

IV. Menores de idade precisam se hospedar junto com um adulto responsável.

V. A quantidade de homens desacompanhados correspondia ao triplo do número de mulheres menores de idade.

Do total de mulheres hospedadas no hotel, qual é a porcentagem de menores de idade?

a) 7%

b) 6%

c) 25%

d) 20%

e) 10%

RESOLUÇÃO:

Podemos representar a situação pelo diagrama a seguir:

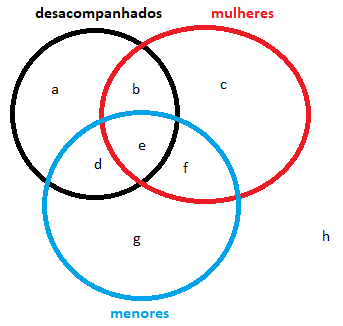
No círculo preto temos as pessoas desacompanhadas. Tudo que está fora dele são pessoas acompanhadas. No círculo vermelho temos as mulheres. Tudo que está fora dele são homens. No círculo azul temos as pessoas menores de idade. Tudo que está fora dele são pessoas maiores de idade.

Com isso em mente, vamos às restrições:

IV. Menores de idade precisam se hospedar junto com um adulto responsável.

–> não existe menor desacompanhado. Logo, d = e = 0.

Ficamos com a seguinte situação:

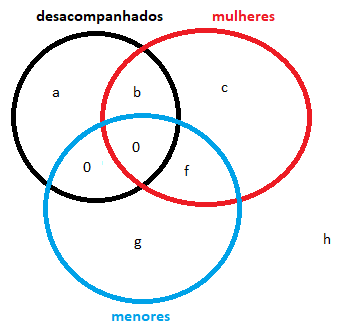
Agora vamos formar nossas equações:

I. 20 se hospedaram desacompanhados.

a + b = 20

b = 20 – a        (i)

V. A quantidade de homens desacompanhados correspondia ao triplo do número de mulheres menores de idade.

a = 3f     (ii)

II. 30 eram do sexo feminino.

b + c + f = 30

(20 – a) + c + f = 30

c = 30 – f + a – 20

c = 10 + a – f 

c = 10 + 2f      (iii)

III. 18 eram menores de idade.

g + f = 18

g = 18 – f      (iv)

São 60 hóspedes no hotel, dos quais 30 são mulheres, o que nos leva a concluir que temos 30 homens:

a + g + h = 30

h = 30 – g – a

h = 30 – a – (18 – f)

h = 30 – a – 18 + f

h = 12 – a + f        (v)

h = 12 – 3f + f

h = 12 – 2f

Repare na equação acima: ela nos diz que o número de homens maiores acompanhados é igual a 12 subtraído de duas vezes o número de mulheres menores acompanhadas. Sabemos que qualquer dessas variáveis não pode ser negativa.

Supondo que f seja zero, teríamos h = 12. Nesse caso a = 0, b = 20, c = 10, g = 18. Qual o problema com esses valores? Não respeitamos a premissa V de que a quantidade de homens desacompanhados correspondia ao triplo do número de mulheres menores de idade.

Supondo que f seja 1, teríamos h = 10. Nesse caso a = 3, b = 17, c = 12, g = 17. Esse seria um cenário possível. No entanto, aqui teríamos um percentual de 1/30 = 3,33% de menores de idade dentre o total de mulheres hospedadas no hotel, sendo que não temos essa opção nas alternativas de resposta.

Supondo que f seja 2, teríamos h = 8. Nesse caso a = 6, b = 14, c = 14, g =  16. Esse seria um cenário possível. No entanto, aqui teríamos um percentual de 2/30 = 6,66% de menores de idade dentre o total de mulheres hospedadas no hotel, sendo que não temos essa opção nas alternativas de resposta.

Supondo que f seja 3, teríamos h = 6. Nesse caso a = 6, b = 11, c = 16, g =  15. Esse seria um cenário possível. Aqui teríamos um percentual de 3/30 = 10% de menores de idade dentre o total de mulheres hospedadas no hotel. –> alternativa E

Supondo que f seja 4, teríamos h = 4. Nesse caso a = 12, b = 8, c = 18, g =  14. Esse seria um cenário possível. No entanto, aqui teríamos um percentual de 4/30 = 13,33% de menores de idade dentre o total de mulheres hospedadas no hotel.

Supondo que f seja 5, teríamos h = 2. Nesse caso a = 15, b = 5, c = 20, g =  13. Esse seria um cenário possível. No entanto, aqui teríamos um percentual de 5/30 = 16,66% de menores de idade dentre o total de mulheres hospedadas no hotel.

Supondo que f seja 6, teríamos h = 0. Nesse caso a = 18, b = 2, c = 22, g =  12. Esse seria um cenário possível. Aqui teríamos um percentual de 6/30 = 20% de menores de idade dentre o total de mulheres hospedadas no hotel. –> alternativa D.

Resposta: D,E (a questão deveria ser anulada)

• ANPAD – 2021)

Um banco liberou para Betina o crédito de R$ 100.000,00 para ser pago pelo Sistema de Amortização Constante em 10 parcelas mensais, sendo a taxa de juros de 5% ao mês.

Analise as afirmativas a seguir sobre as prestações que Betina deve pagar ao banco.

I. O valor das prestações a serem pagas não se altera ao longo dos meses.

II. O valor da amortização na terceira parcela do pagamento é igual a R$ 10.000,00.

III. Ao liquidar a dívida com o banco, Betina terá pagado só de juros um total de R$ 27.500,00.

É correto o que se afirma em:

a) II, apenas.

b) I, apenas.

c) I e III, apenas.

d) I, II e III.

e) II e III, apenas.

RESOLUÇÃO:

Analisando as afirmativas, temos:

I. O valor das prestações a serem pagas não se altera ao longo dos meses.

O valor da amortização é constante. Já as prestações se alteram ao longo dos meses. Afirmativa falsa.

II. O valor da amortização na terceira parcela do pagamento é igual a R$ 10.000,00.

Como a amortização é constante ao longo das 10 parcelas, ela será igual a 100.000/10 = 10.000 reais. Portanto, na terceira, a amortização também será de 10 mil reais. Afirmativa verdadeira.

III. Ao liquidar a dívida com o banco, Betina terá pagado só de juros um total de R$ 27.500,00.

Assim, chegamos na seguinte tabela:

Nº parcela	Saldo Devedor	Amortização	Juros	Parcela
1	100000	10000	5000	15000
2	90000	10000	4500	14500
3	80000	10000	4000	14000
4	70000	10000	3500	13500
5	60000	10000	3000	13000
6	50000	10000	2500	12500
7	40000	10000	2000	12000
8	30000	10000	1500	11500
9	20000	10000	1000	11000
10	10000	10000	500	10500

Se somarmos a coluna juros, concluiremos que, de fato, o total pago a título de juros é 27.500 reais. Afirmativa correta.

Resposta: E

Não deixe de conferir nossos cursos para a ANPAD e bons estudos!

550 questões resolvidas (em PDF) de Raciocínio Lógico, Analítico e Quantitativo para Teste ANPAD

Raciocínio Quantitativo (Teoria e 259 questões Anpad resolvidas) para Teste ANPAD – Orientação Acadêmica

Raciocínio Lógico e Raciocínio Analítico (Teoria e 331 questões Anpad resolvidas) para Teste ANPAD – Orientação Acadêmica